The Travelling Salesman Problem (TSP) is a well-known NP-hard problem: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?

In this report, I attempt to solve the TSP using heuristics with approximation guarantees algorithm, then conduct experiments and make analysis of the performance of the program.

Problem Definition

The TSP problem is defined as follows: Given a graph $G=(V,E)$ where $V$ is a set of $n$ vertices and $E$ is a set of edges, find the shortest simple cycle that visits all $n$ vertices once and only once.

Related Work

To calculate MST-Approximation, we have to compute a MST for the graph first, one lower bound of the TSP tour is the sum of edges in MST. Next, we double the edge to convert the MST into a directed graph, and we can skip visited vertices while constructing the TSP tour to get a smaller path due to triangle inequality. So this algorithm is guaranteed to have an approximation ratio of 2.

Christofied[1] optimized the MST-Approximation method which guaranteed an approximation ratio atmost 1.5. The blossom algorithm[2] based on primal-dual method[3] can also give a better solution.

Algorithm

For approximation, we use the minimum spanning tree to construct the TSP tour. The definition of a minimum spanning tree is that: Given an connected, undirected graph $G = (V,E)$ where $V$ is the set of pins and $E$ is the set of possible interconnections between each pair of pins, and for each edge $(u,v)\in E$, we have a weight specifying the cost to connect $u$ and $v$. The goal is to find an acyclic subset $T\subset E$ that connects all the vertices and whose total weight $w(T) = \sum_{(u,v)\in T} w(u,v)$ is minimized[4].

From the definition, we can know that the lower bound of MST-Approximation algorithm will be the total weight of the minimum spanning tree. So firstly, we have to generate a minimum spanning tree and here, due to our graph is a fully connected graph, we choose the prim algorithm. And the next step is to construct a TSP tour from the MST. Assume all the edges are symmetric and fulfill the triangle inequality: $w(u,v)\leq w(u,w)+w(w,v), \forall u,v,w\in V$. To construct the TSP tour, use edges in MST as much as possible but still keeping the tour a simple cycle. The strategy here is to choose a root, and follow the MST along the edge: only add a vertex as part of the TSP tour the first time it is encountered, that is, short cut multiple edges whenever there are repeated vertices[5].

Pseudocode

Input: A connected, undirected graph G=(V,E)
Output: A TSP tour
Function: MST(G)
	V_new = s // s is a randomly chosen start point
	E_new = {}
	while V_new != V:
		// u is a node in V_new, v is a node in V-V_new
		(u, v) = argmin(E)
		V_new.add(u)
		E_new.add((u, v))
	return mst

Function: Tour(mst, tour, s)
	if s is not in tour:
		tour.append(s)
		u = s
		next = arg(u, v)
		for node in next:
			Approx(mst, tour, node)

Function: Approx(G)
	mst = MST(G)
	tour = {}
	s
	Tour(mst, tour, s)
	return tour

Complexity

Space complexity

While generating the MST, we use the prim algorithm and use a 2-dimension matrix to store the distances between each pair of nodes. We also use a list to store all the vertices that have been visited which will eventually at the size of $n$, where $n$ is the number of vertices(cities). We also use a list to store the MST whose size is $n-1$. In order to get the TSP tour from the MST, we also need a list of size $n+1$ to store the result. So in general, the space complexity is $O(n)$.

Time complexity

While generating the MST, we have to go through all the vertices to find it’s smallest edge which will take $n$ loops. In each loop, we have to find the smallest distance from the vertex to other vertices which takes constant time since we use the “unravel_index” method in python to get the location of the smallest value in our distance matrix. But we have to set distance between visited vertices to $inf$ which will take $O(n)$ time for the worst case. So the total time of generating a MST will be of $O(n^2)$. To construct the TSP tour from MST, we will also need $n$ loops and in each loop, we may need $O(n)$ time for the worst case(all other vertices are connected to the same one vertex in the MST), so the time complexity for tour function is also $O(n^2)$. So the overall time complexity is $O(n^2)$.

Approximation Proof

Since $MST$ is the lower bound, we have:

$ cost(MST)\leq OPT $

$MST^$ is a tour use all the $MST$ edges twice and meet every vertex twice: $ cost(MST^) = 2cost(MST) $

Because of triangle inequality, we have: $ cost(tour) \leq cost(MST^*) $

According to above inequalities, we have: $ cost(tour)\leq cost(MST^*) = 2cost(MST) \leq 2OPT $

Empirical Evaluation

Our MST-Approximation algorithm runs with an approximation ratio of atmost 1.45: $cost(tour)\leq 1.45OPT$ which fulfill our theoretical approximation ratio of 2.

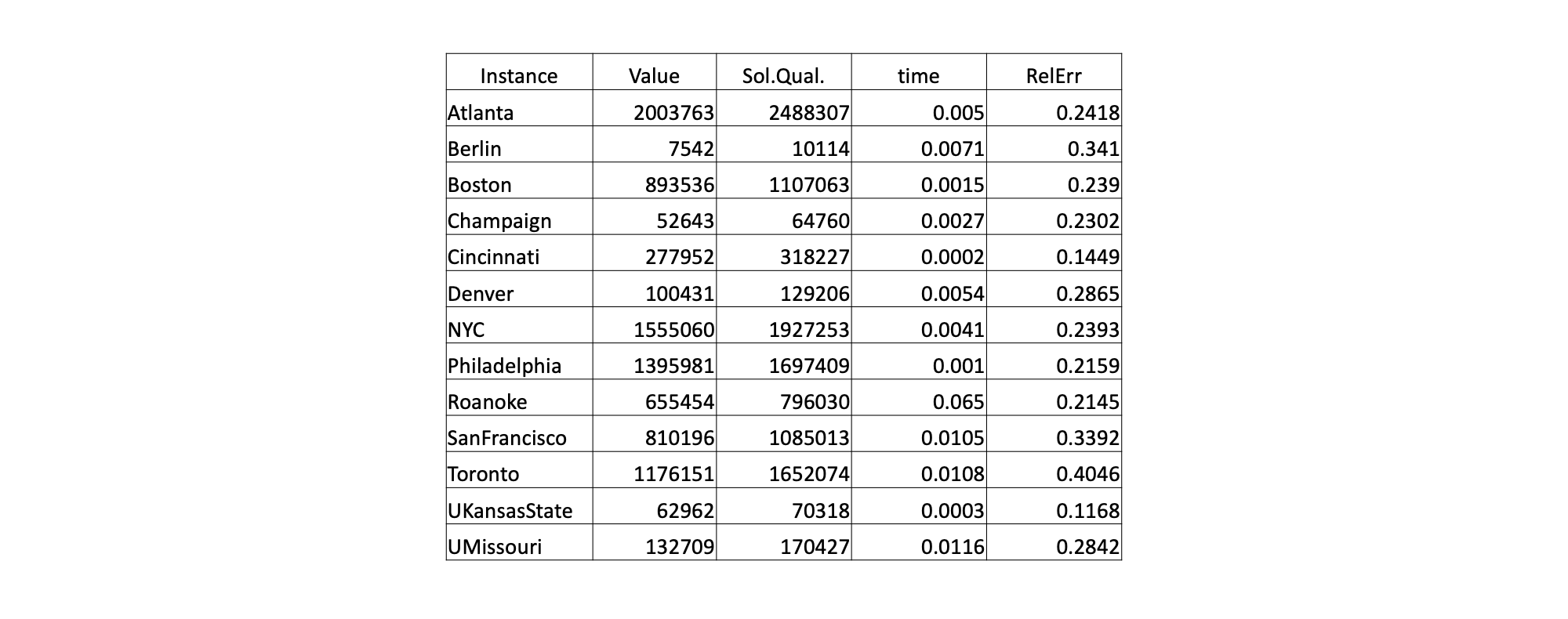
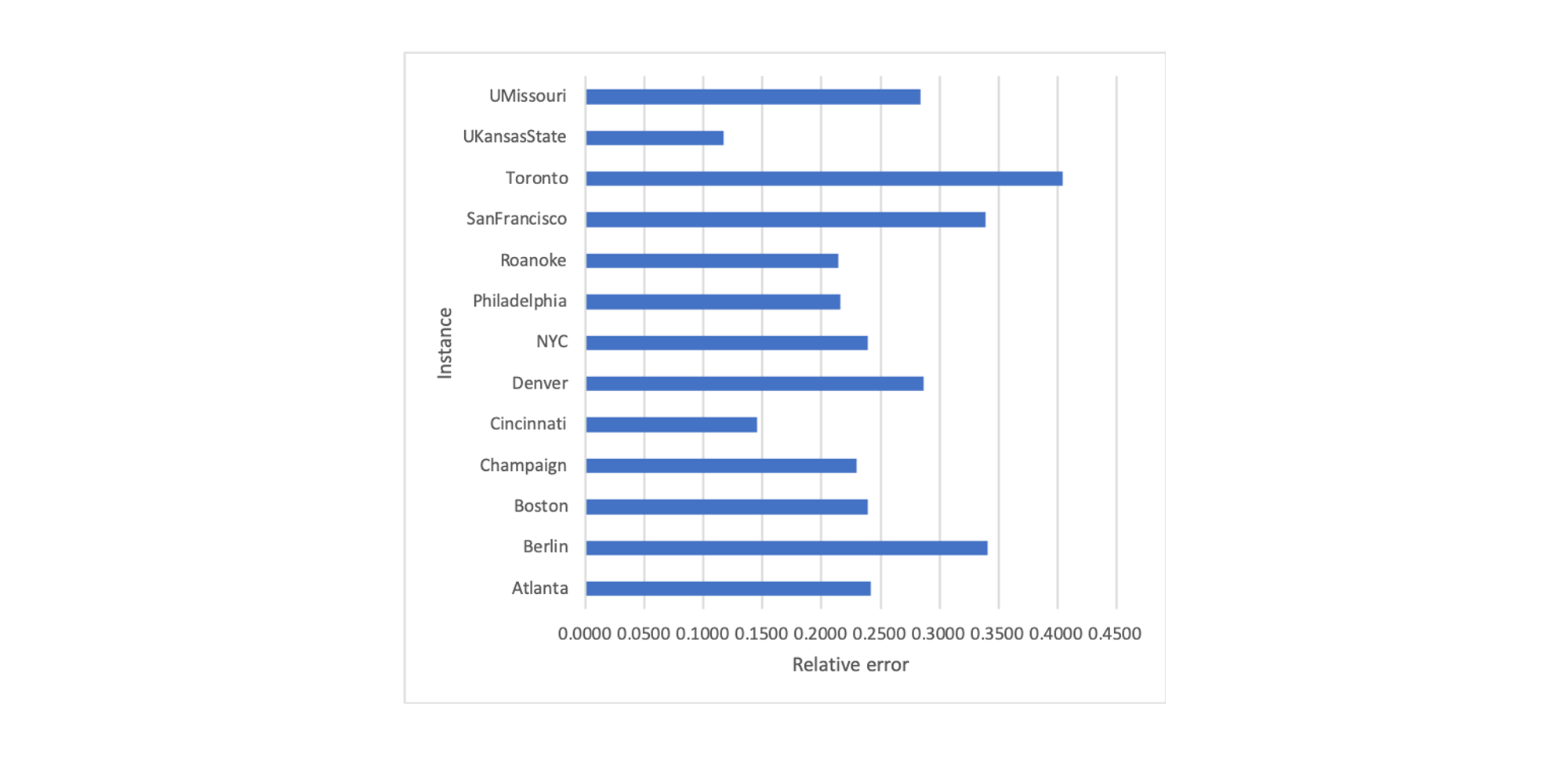
From the result, we can also see that the Relative error doesn’t have much to do with the size of instances.

Here is a diagram of Relative error of difference cities.

Discussion

As we can see from the result, the MST-Approx can guarantee a approximation ratio of 2, and it can derive the result quickly, but the relative error is quite large since we randomly choose a start point to find a tour from the MST which may lead to some bad solutions while shortcutting edges. One way to deal with this problem is that we can start from every vertex and record the quality of each start point, then we can choose the shortest tour. In this way, the approximation ratio is still 2 but we may get a better result.

A way to improve the MST-Approx method is that we can use the Christofides algorithm[1] to find Min Cost Perfect Matching on all the vertices with odd degree int the MST which can guarantee an approximation ratio of 1.5.

References

[1] Nicos Christofides. 1976. Worst-Case Analysis of a New Heuristic for the TravellingSalesman Problem.

[2] Jack Edmonds. 1965. Paths, Trees, and Flowers.Canadian Journal of Mathematics17 (1965), 449–467. https://doi.org/10.4153/CJM-1965-045-4

[3] Michel X Goemans and David P Williamson. 1997. The primal-dual methodfor approximation algorithms and its application to network design problems. Approximation algorithms for NP-hard problems(1997), 144–191.