The program implements an event-driven, discrete event simulation to simulate queueing networks using given configuration file. The simulator includes three different types of components: Generator, Exit, Queueing Station. Each component has some number of input and output ports through which customers arrive and depart. For example, assume customers require a negligible amount of time to travel between components. The generator creates a new customer with average interarrival time (a random number generator following an exponential distribution.). The generator then sends customers flow to service station. The customer then is routed to another station with probability

API and Simulation Model

The program uses arrComp array to store all components in the system, FEL to store event using timestamp as the priority. The first part finished in this project is the construction of model. The program first reads the configuration file to model Simulation model. It includes a set of state variables that represent the current state of the system being modeled. It also includes functions and event handler procedures. The event handler procedures procedures collectively model the operation of the system being simulated. To develop the simulation application, configuration file are used to define the state variables and the different types of events that are modeled. This program implements three event functions to handle different event types.

First, the configuration program reads in the configuration information. When it encounters identification characters for different components, it calls different component producers: makeGenerator, makeExit, makeSta. In the makeGenerator function. The program allocates a new generator. The generator constructor takes the generation time and destination component ID as parameters. Then the function adds this generator into the list of components. And the function created an EventData and schedule this generation event into the FEL.

In the makeSta function. Customers in a station component are stored in a FIFO queue. This function allocates space for a new station. The station constructor takes parameter including the average serve time and destination ID, corresponding probabilities. It stores destination components and corresponding probability in array. Then the function adds this station into the list of components.

The makeExit function records the total number of customers that have exited at this exit.

After the construction of the model. The program uses event handler to procedure events modeled by the simulation. The event handler procedures collectively model the operation of the system being simulated. To develop the simulation process, the program takes and updates state variables and the different types of events. The program implements different functions for each different event type.

Simulation engine parts includes a data structure called the future event list (FEL) that is a priority queue that contains the set of events waiting to be processed. The simulation engine holds the main event processing loop which repeatedly (1) removes the smallest timestamped event from the FEL, and (2) calls a function (defined in the simulation application) to simulate three kinds of events: generate, arrival, departure.

The loop continues processing events until the simulation time reaches the time limit given in the configuration file. The simulation maintains a clock variable indicating how far the simulation has advanced in simulation time. It also includes a function called by the simulation application to schedule a new event, i.e., to allocate memory for the event, fill in various parameters, and insert the new event into the FEL.

Generate Event

It involves adding a new customer into the system, generating the subsequent arrival event, and producing a new generation event. This function creates a new customer and recording the generation time. Then the customer will be sent to a destination station and become an arrival event. Then, the generator processes next generation following an exponential distribution.

Arrival Event

If the event arrivals at the exit. The global variable recording the total number of customers having left the system is updated. Else, the customer arrives at a station, if there is no other customer waiting in the queue, it will get served immediately. Or it will be added into the waiting queue.

Departure Event:

If there is only one customer waiting in the queue, this customer will get served and be sent to another station dependent of the probability stored in the array. If there is more than one customer in the queue. The one in the head of the queue will get served and pointer will be moved to point to the next customer.

Simulation Study

We construct a simulation to analyze the operation of a food court. The food court includes:

1. A queueing station where customers enter and receive a tray to carry their food; assume the mean service time for this station is 0.1 minutes.
2. Four queueing stations (A, B, C, D) each serving a different type of food. Assume the popularity (i.e., the probability a customer will select that station) of stations A, C, and D are the same, but station B is twice as popular as the others. The average service time of these stations are: A: 3.2; B: 1.7; C: 3.3; D: 2.8.
3. Two beverage stations where beverages are obtained, after obtaining food. Assume all customers purchase one beverage and each customer is equally likely to select either station. The average service time of the beverage station is 0.5 minute.
4. One or more check out stations where customers must pay for their food. Each check out station has an average service time of 1.0 minute. Assume a customer is equally likely to select any check out station. After departing the check out station, most customers (95%) will exit the system. However, the remaining customers (5%) will find they do not have sufficient funds to pay for their food. In this case, their food order will be left at the check out station, and the customer will go back to make another food order. Specifically, the customer will bypass the station for picking up a tray, randomly select one of the four queueing stations (using the same probabilities as reported earlier) and proceed directly to that station to get a new order of food and then get a new beverage.

According to this, we construct our config file as:

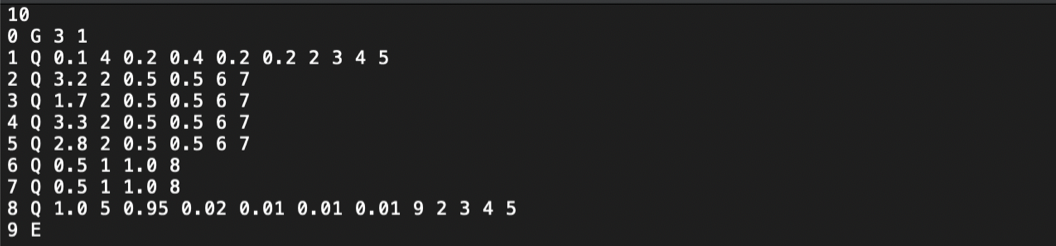
The first line indicates the number of components in the configuration file. The second line means this is a generator with ID 0 and interarrival time 3, the customers go straight into station 1. The third line means that the average service time of this station is 0.1, and customers depart from this station may go to station 2 with probability 0.4, or station 3, 4, 5 with probability 0.2 for each station. The last line indicates this is an exit and if a customer arrives here, he/she will leave the food court. In this configuration file, we only have 1 check out station (station ID 8), we also construct 24 other configuration files with different interarrival time of customers and different number of check out stations. And here are the results.

First, we compare the results of different number of check out stations from 1 to 5. In this case, we assume the interarrival time of customers is 3.

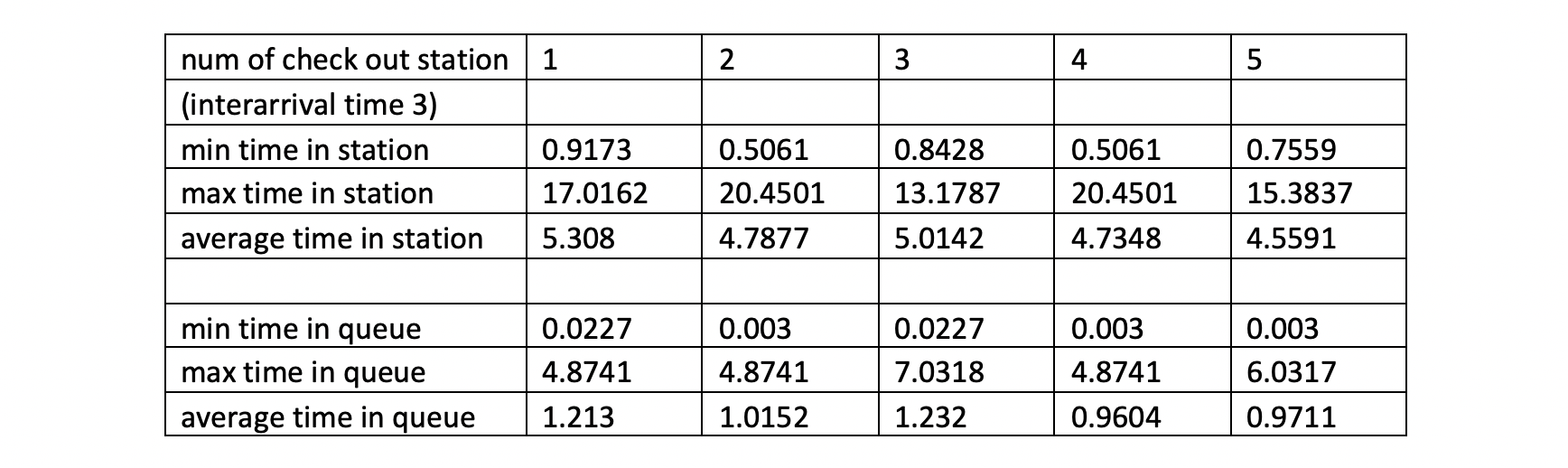
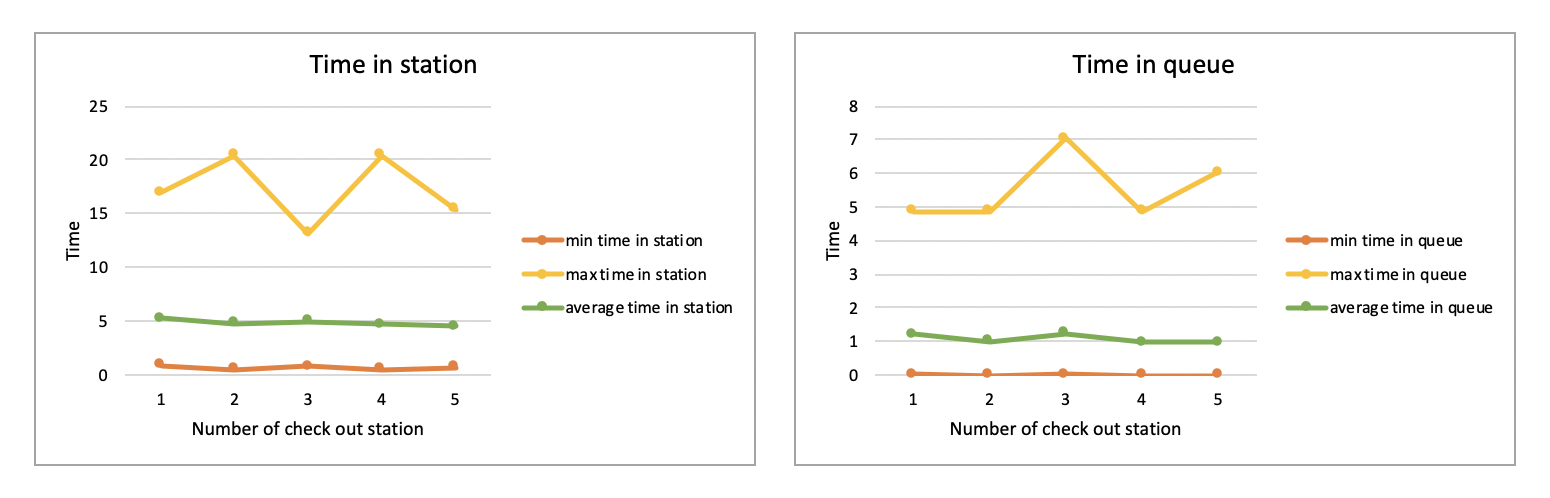
According to the table and the plot, we can see that the maximum time and the minimum time of a customer remains in the station is not strictly related to the number of check out stations, but as the number of check out station grows, the average time of a customer remains in the station decreases. This is similar to the reality since them more check out there are, the less time each customer has to wait to check out. We can see that the maximum time and the minimum time of a customer stays in the queue is the also kind of random, but the average time a customer stays in the queue generally decreases as the number of check out stations grows.

We also compare the behaviors of different interarrival times from 0.1 to 5 with different number of check out station.

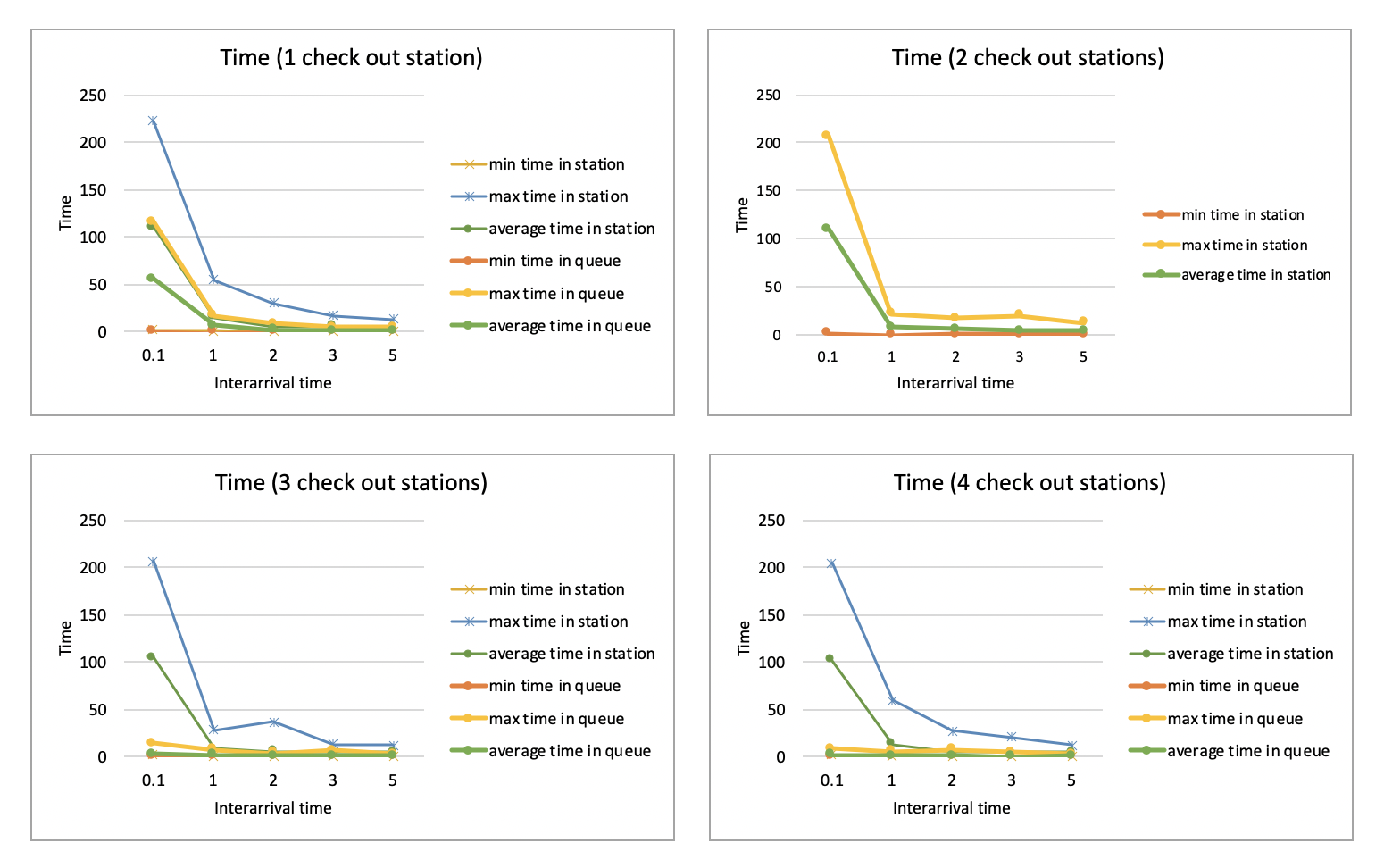
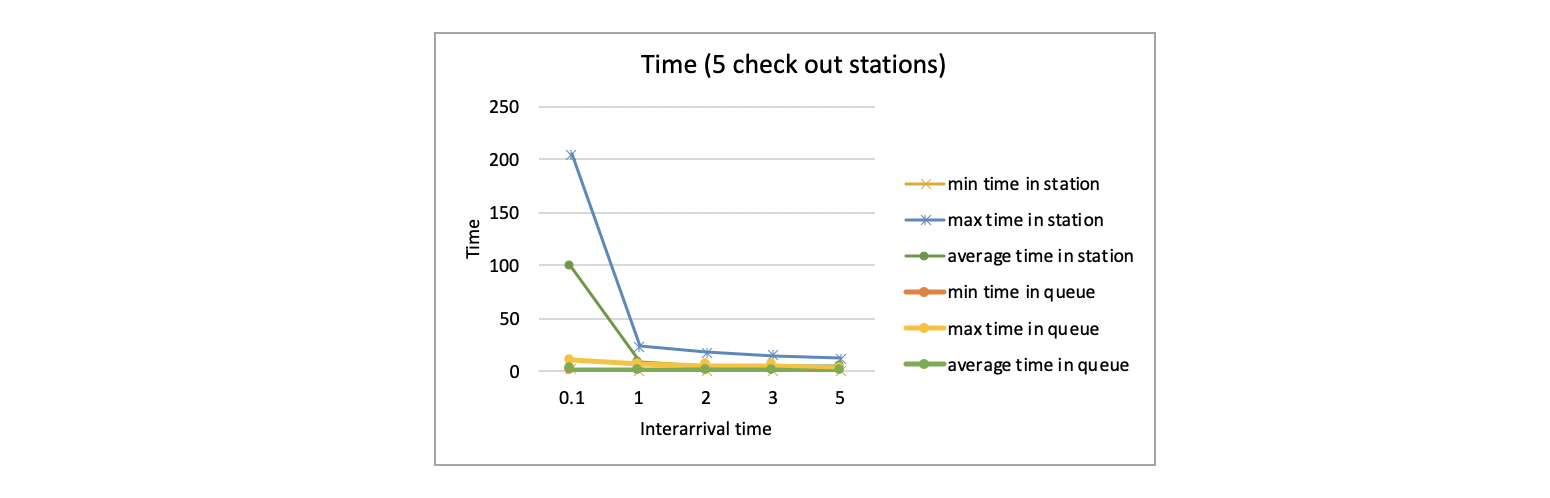
From the above 5 pictures, we can see that when the interarrival time is small, that is, the rate of customers entering the system is large, the maximum time and the average time of a customer stays in the station is huge. This reflects the reality, if there are too many customers, the time each customer has to wait will be much longer than usual.